EM算法

前几天，和一个老师线上面试，我说我用GMM做过相关项目，他就顺着这条线，问了我项目的pipeline，然后问我GMM中怎样确定高斯混合成分，我就说用train数据训练，test数据确定参数，他嗯了一声，我感觉不对，模型的超参选择怎么能依靠test呢？还好在老师的引导下，想起来valid数据的作用。之后，他又问我，GMM的输出是先验概率还是后验概率？我一脸懵逼，猜了后验概率，他顺着问我，那这个模型中什么是先验概率？额，我不知道，实在没弄清楚，他评价了一句，“你们概率论学了不用吗？”。之后，又问了我卷积与梯度的相关问题，就不多说了。电话面试虽然通过了，后续面试就难了，为了好好准备面试并且说明我不是调包程序员，我要认真学习机器学习的算法了。因为GMM模型是用EM算法迭代求解的，所以我首先学习EM算法。

EM算法初识

EM算法也称为期望极大算法。它是一种迭代算法，用于含有隐变量的概率模型参数估计。EM算法的每次迭代由两步组成：E步求期望；M步求极大。求什么期望？又极大化什么呢？我们慢慢看。

通常对于概率模型的参数估计，可以使用极大似然估计法或者贝叶斯估计法来估计模型参数。但是当模型含有隐变量时，这种方法就行不通了，可以看看这篇blog来理解隐变量的含义。

Jensen 不等式

设$ f $是定义域为实数的函数，如果对于所有的实数$x$，它的二阶导 $f^{''}(x) \ge 0$ ，则说明该函数为凸函数。当 $f^{''}(x) > 0$ ，则说明该函数为严格凸函数。

Jensen不等式：假设 $f$ 是凸函数， $X$ 是随机变量，则有： $E[f(x)] \ge f(EX)$ ，其中EX为随机变量X的期望，这里简写。

如果$f$是严格的凸函数，那么上述等式当且仅当X为常数的时候取等。用图来理解这个不等式：

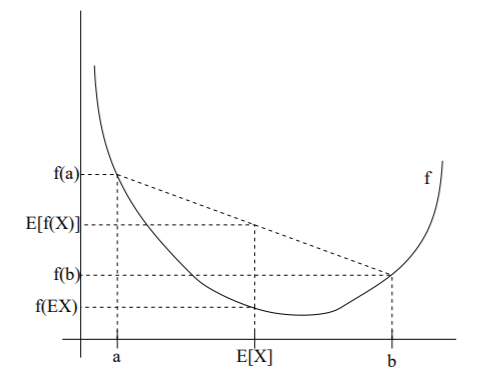
当$f$是凹函数的时候，不等式取反就可以了，即 $E[f(x)] \leq f(EX)$ 。

EM算法理论推导

这部分理论推导，我参照了Andrew Ng以及李航的统计学习方法，建议有能力者，直接看Andrew Ng的材料。

给定训练样本集 ${x_1, x_2, x_3...x_m}$ ，样本间彼此独立，我们假设隐变量为 $z$ ，则 $x$ 的密度函数为：

$p(x,\theta)=\sum_{z} p(x,z;\theta) \tag{1}$

我们希望极大化对数似然函数，来得到参数 $\theta$ 的估计：

$l(\theta)=\sum_{i=1}^n logp(x^{(i)};\theta) \tag{2}$

考虑隐变量z， $(2)$ 式可以写成：

$l(\theta) = \sum_{i=1}^n logp(x^{(i)};\theta)=\sum_{i=1}^n log\sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) \tag{3}$

直接求上式的解析解是比较困难的，一是因为上式包含隐变量 $z$ ，二是上式涉及对数函数的求和，很难求导。在这样的背景下，EM算法给出了高效的方法来最大化对数似然函数，得到模型参数的近似解。为了后续描述方便，我们考虑一个样本 $x$ 的对数似然函数，整个样本集，只不过是对单一样本的求和。

$logp(x;\theta)=log\sum_{z} p(x,z;\theta) \tag{4}$

我们假设 $Q$ 是z的分布函数。即： $\sum_{z} Q(z)=1, Q(z)\ge 0$

将 $(4)$ 式转化一下：

$log p(x;\theta) = log \sum_{z} p(x,z;\theta) = log\sum_{z} Q(z)\frac{p(x,z;\theta)}{Q(z)} \ge \sum_{z} Q(z)log\frac{p(x,z;\theta)}{Q(z)} \tag{5}$

第一步等式转化好理解，分子分母同时乘一个 $Q(z)$ ，第二步不等式转化用到了前面所说的Jensen不等式。 $log$ 函数是凹函数，则有 $E[f(x)] \leq f(EX)$ ，将 $\frac{p(x,z;\theta)}{Q(z)}$ 当作随机变量， $Q(z)$ 当作随机变量的分布函数，就可以推导第二步的不等式。

如果我们知道 $Q$ ,就可以直接求出 $\theta$ 。如果我们知道 $\theta$ ，就可以推导出 $Q$ 。好了，现在 $Q$ 和 $\theta$ 都不知道，怎么办？那就猜吧（这不是我们经常干的事嘛），我们先猜一个 $\theta$ ，也就是说，我们给模型的参数一个初始值，有了初始值后，我们想极大化对数似然函数，考虑上面我们已经推导了对数似然函数的下界，因此我们很自然的想到了水涨船高，于是极大化这个下界。不等式取等的时候，下界最大，考虑Jensen不等式取等的条件，随机变量为常数，即：

$\frac{p(x,z;\theta)}{Q(z)} = c$

也就是说： $Q(z) \propto p(x,z;\theta)$ ，那么 $Q(z)$ 可以表示成：

$Q(z)=\frac{p(x,z;\theta)}{\sum_z p(x,z;\theta)}=\frac{p(x,z;\theta)}{p(x;\theta)} = p(z|x;\theta) \tag{6}$

也就是说当 $Q$ 是 $x,\theta$ 确定时的后验概率分布，不等式取等。

为了方便，我们将 $(5)$ 式称作evidence lower bound(ELBO)，因此：

$ELBO(x;Q,\theta)=\sum_{z} Q(z)log\frac{p(x,z;\theta)}{Q(z)} \tag{7}$

有了这个式子后，我们重写 $(5)$ 式:

$\forall Q,\theta,x, logp(x,\theta) \ge ELBO(x;Q,\theta) \tag{8}$

EM算法就是交换的更新 $Q$ 和 $\theta$ 。E步：在 $\theta$ 确定的情况下，根据 $(8)$ 式计算出 $Q$ 。M步：固定 $Q$ ，最大化 $ELBO$ ，得到 $\theta$ 的更新值。回到E步。

前面的谈论都是基于一个样本的，现在考虑整个样本集：

$l(\theta) \ge \sum_i ELBO(x^{(i)}; Q_i, \theta)=\sum_i \sum_{z^{(i)}} log Q_i(z^{(i)}) \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \tag{9}$

根据 $(6)$ 式，得到 $Q$ ：

$Q_i(z^{(i)}) = p(z^{(i)}|x^{(i)};\theta)$

下面给出算法：

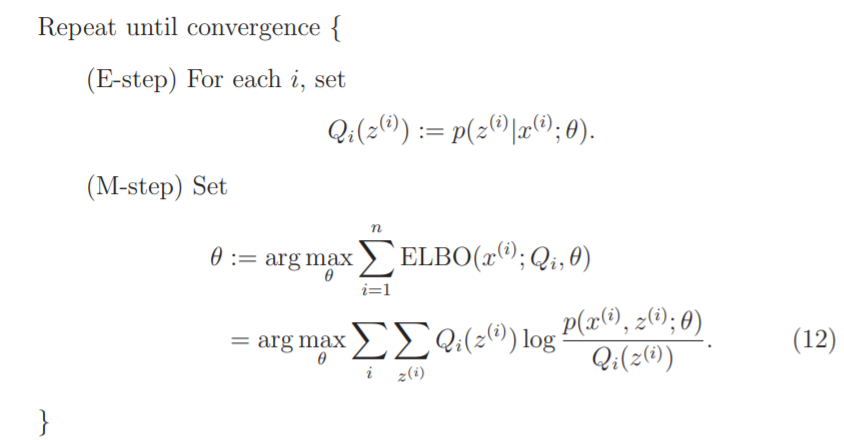
我们怎么知道算法收敛呢？如果我们能证明 $l(\theta^{(t)}) \le l(\theta^{(t+1)})$ ，就能说明极大似然值单调递增，也就能确保收敛性了。

在第t+1次迭代E步时候，我们知道根据 $\theta^{(t)}$ ，确定 $Q_i^{(i)})$ (第i个样本Q的后验概率)，因为 $Q_i^{(i)})$ 是根据等式取等推出来的，此时有：

$l(\theta^{(t)})=\sum_i^n ELBO(x^{(i)}; Q_i^{(t)}, \theta^{(t)})$

在第t+1次迭代M步时候，我们知道固定 $Q_i^{(i)})$ ，求 $\theta^{(t+1)}$ ，是ELBO极大化，则：

$\sum_i^n ELBO(x^{(i)}; Q_i^{(t)}, \theta^{(t+1)}\ge\sum_i^n ELBO(x^{(i)}; Q_i^{(t)}, \theta^{(t)})$

在第t+2次迭代的E步，有：

$l(\theta^{(t+1)})=\sum_i^n ELBO(x^{(i)}; Q_i^{(t+1)}, \theta^{(t+1)})\ge\sum_i^n ELBO(x^{(i)}; Q_i^{(t)}, \theta^{(t+1)})$

这就证明了算法的收敛性。

总结

我们回头看一下算法流程。我们的目的是极大化似然函数，但是由于隐变量和求和的存在导致很难直接极大化似然函数。因此，我们初始化模型参数，得到隐变量的后验概率，再固定隐变量后验概率，更新模型参数使似然函数极大化，然后根据更新的参数，再更新隐变量的后验概率。反复迭代，直到模型收敛。下一篇，我们会说明GMM模型，并用EM计算它的参数，如果有可能，我尝试撸一套纯python代码，不过，目前基本不可能，哈哈。

Reference

http://cs229.stanford.edu/notes-spring2019/cs229-notes8-2.pdf https://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html https://blog.csdn.net/liu1194397014/arti4cle/details/52766760 https://blog.csdn.net/zouxy09/article/details/8537620

My Blog

Work hard, play hard !

EM算法

EM算法初识

Jensen 不等式

EM算法理论推导

总结

Reference